Enhancing finance risk-based portfolios with quantum technology

Portfolio optimization is a crucial process in investment management. It aims to construct an optimal portfolio by considering various factors such as risk, return, and diversification. The goal is to find the most efficient allocation of assets that maximizes potential returns while minimizing the associated risks.

One popular approach to constructing efficient portfolios is by applying risk parity strategies. Among various risk parity methodologies, Hierarchical Risk Parity (HRP) has emerged as a powerful technique for effectively allocating assets based on their risk contributions within a hierarchical framework.

Optimizing financial portfolios

Modern Portfolio Theory (MPT) is one of the most influential economic theories in finance and investment. Pioneered by Harry Markowitz (1952), the theory suggests that stock portfolio diversification can reduce risk. Its main objective was to define an investment portfolio with efficient assets that would allow a minimum risk level for an expected return level. Unfortunately, although successful, the theory was based on simple approaches that didn’t consider the correlation between assets and was contested by investors.

The HRP allocation algorithm developed by Marcos López de Prado (2016) considers the individual volatilities of assets and their interrelationships and dependencies. By considering the correlation structure among assets, HRP aims to achieve a more robust and diversified portfolio allocation, particularly for coping with market turbulences and systemic risks.

At its core, HRP involves three key steps:

1. Hierarchical clustering
2. Quasi-diagonalization of the asset correlation matrix, and
3. Recursive bisection and assets weights computation.

In the first step, assets are grouped based on their correlation matrix. This hierarchical clustering approach captures the underlying structure of the asset universe, allowing for a more intuitive representation of relationships between assets.

Once the hierarchical structure is established, the quasi-diagonalization step comes into play. It consists of finding the correlation matrix’s reordering that transforms it into the most block-diagonal matrix possible. This task is known to be NP-hard —the kind of task that Qaptiva™, our quantum emulation platform, can solve efficiently.

Finally, the risk allocation step assigns risk contributions to each cluster and then distributes them to the individual assets within each cluster. The allocation is determined by a measure of risk contribution, which considers both the volatility and correlation of the assets. This ensures that risk is allocated in a manner that reflects the diversification potential of each asset and the relationships between them.

Leveraging quantum computing to solve complex problems

The quasi-diagonalization problem is formulated as a Quadratic Unconstrained Binary Optimization (QUBO) problem. In general, a QUBO model can be written as the minimization of a cost function q:

Where are binary variables and is a real symmetric matrix.

Qaptiva^TM, the quantum computing offer from Eviden, allows using all the main quantum programming paradigms. For the quantum-inspired HRP algorithm, as for any combinatorial optimization problem, two of them are well-suited. These are the gate-based quantum circuits and quantum annealing.

Quantum-inspired Hierarchical Risk Parity

Conventional algorithms involve the inversion of the covariance matrix, making them unstable in the volatile stock market. In contrast, the QHRP algorithm computes a hierarchical tree from the correlation matrix without the need to invert it.

The goal is to find the reordering of assets for the correlation matrix that transforms the correlation matrix into the most block-diagonal matrix possible. To achieve this, a measure is introduced that weighs matrix elements depending on their distances to the diagonal. This can be formulated as follows:

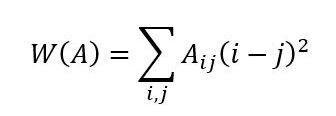
Where are absolute values of the covariance elements matrix so that .

From this metric, we can define an objective function to minimize, resulting in the most block-diagonal matrix. However, we also must add a constraint to ensure each asset  is allocated to only one new position, and each new position  is populated by only one asset, formulated as below:

By combining the objective function and the constraints, we can build a QUBO problem of size which can be solved on Qaptiva^TM platform using Simulated Quantum Annealing.

Solving problems without the limitation of variable interactions

QUBO problems are suited to be solved on Quantum Annealers, but in practice, they are limited in terms of qubits connectivity. Qubits have a limited number of neighbors they can interact with, and the connectivity is directly related to the number of quadratic terms a variable can have. Quantum Annealers are also limited in the number of qubits, limiting the problem size.

In the case of QHRP, each variable is linked to all other variables of the problem by a quadratic term, meaning that it requires an all-to-all QPU topology, which does not exist practically, making the QHRP unsolvable on a real Quantum Annealer.

Qaptiva^TM emulates the quantum annealing process without hardware constraints. Thus, it allows solving problems without the limitation of variable interactions, with an unmatched number of variables, and faster than classical simulated annealing.

Eviden’s new quantum computing offering, Qaptiva^TM, allows to address other financial use cases and provides dedicated software libraries to solve complex issues related to portfolio optimization, optimal feature selection in credit scoring, and fraud detection.